Introduction To Arrays

MATLAB Programming/Arrays/Introduction to Array Operations

Introduction to array operations

As arrays are the basic data structure in MATLAB, it is important to understand how to use them effectively. See the previous section for that.

Arrays in MATLAB obey the same rule as their mathematical counterpart: by default, thematrix definitions of operations are used, unless a special operator called the dot operator is applied.

Because arrays operations are so similar to the equivalent mathematical operations, a basic knowledge of linear algebra is mandatory to use matlab effectively. However, we won't be as precise as in mathematics when using the terms vector and matrix. In MATLAB, both are arrays of doubles (thus being a matrix in the real mathematical meaning), and MATLAB considers vectors as a matrices with only one row or only one column. However, there are special functions just for vectors; see the vector module for an explanation of how to use these.

Basics

Accessing elements of a matrix

Using a Single Index

Now that you know how to define a simple array, you should know how to access its elements. Accessing the content of an array is done through the operator (), with the index inside the parenthesis; the indexing of the first element is 1:

>> a = [1, 2, 3];
>> a(1)
 
ans =

    1

>> a(3)

ans =

    3

Accessing an element outside the bounds will result in an error:

>> a(5)
???  Index exceeds matrix dimensions.

Using Multiple Indexes

To access a single matrix element, you can use the (i,j) subscript, where i is the index in the row, and j in the column:

>> a= [1, 2; 3, 4];
>> a(1, 2)

ans = 

    2

>> a(2, 1)
 
ans = 

    3

Using A Unique Index

You can also access a matrix element through a unique index; in this case, the order is column major, meaning you first go through all elements of the first column, then the 2d column, etc... The column major mode is the same as in Fortran, and the contrary of the order in the C language.

>> a = [1, 2, 3; 4, 5, 6];
>> a(3)

ans =

    2

Using a Colon (:) for a Block Index

It is also possible to access blocks of matrices using the colon (:) operator. This operator is like a wildcard; it tells MATLAB that you want all elements of a given dimension or with indices between two given values. For example, say you want to access the entire first row of matrix a above, but not the second row. Then you can write:

>> a = [1, 2, 3; 4, 5, 6];
>> a(1,:) %row 1, every column
ans = 
   1     2     3

Now say you only want the first two elements in the first row. To do this, use the following syntax:

>> a = [1, 2, 3; 4, 5, 6];
>> a(1, 1:2)
ans = 
   1     2

The syntax a(:) changes a into a column vector (column major):

>> a = [1, 2, 3; 4, 5, 6]
>> a(:)
ans = 
   1
   4
   2
   5
   3
   6

Using the end Operator

Finally, if you do not know the size of an array but wish to access all elements from a certain index until the end of the array, use the end operator, as in

>> a = [1, 2, 3; 4, 5, 6]
>> a(1, 2:end) %row 1, columns from 2 until end of the array
ans =
   2     3

Logical Addressing

In addition to index addressing, you can also access only elements of an array that satisfy some logical criterion. For example, suppose a = [1.1, 2.1, 3.2, 4.5] and you only want the values between 2 and 4. Then you can achieve this in two ways. The first is to use the find function to find the indices of all numbers between 2 and 4 in the array, and then address the array with those indices:

>> a = [1.1, 2.1, 3.2, 4.5];
>> INDICES = find(a >= 2 & a <= 4);
>> a(INDICES)
ans =
   2.1   3.2

This does not work in MATLAB 2006b.

The second method is to use logical addressing, which first changes a into a logical array, with value 1 if the logical expression is true and 0 if it is false. It then finds and returns all values in the a which are true. The syntax for this is as follows:

>> a = [1.1, 2.1, 3.2, 4.5];
>> a(a >= 2 & a <= 4)
ans =
   2.1   3.2

Basic operations

Rational Operators on Arrays

Addition and Subtraction

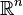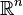The interesting part is of course applying some operations on those arrays. You can for example use the classic arithmetic operations + and - on any array in matlab: this results in the vector addition and subtraction as defined in classic vector vectors spaces , which is simply the addition and subtraction elements wise:

>> [1, 2, 3] - [1, 2, 1]

ans = 
 
   0   0   2

Multiplication by a Scalar

The multiplication by a scalar also works as expected:

>> 2 * [1, 2, 3] 

ans = 

   [2, 4, 6]

Multiplying and Dividing Arrays

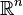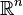Multiplication and division are more problematic: multiplying two vectors in  does not make sense. It makes sense only in the matrix context. Using the symbol * in matlab computes the matrix product, which is only defined when the number of columns of the left operand matches the number of rows of the right operand:

>> a = [1, 2; 3, 4];
>> a * a

ans =

    7    10
   15    22

>> a = [1, 2, 3]; b = [1; 2; 3];
>> a * a
??? Error using ==> *
Inner matrix dimensions must agree.
>> a * b

ans =

   14

Using the division symbol / has even more constraints, as it imposes the right operand to be invertible . For square matrices,  is equivalent to . For example :

>> a = [1, 2; 3, 4]; b = [1, 2; 1, 2]
>> b / a

ans =

    1     0
    1     0

>> a / b
Warning: Matrix is singular to working precision.

ans =

  Inf   Inf
  Inf   Inf

Component-wise Operations

If you desire to multiply or divide two matrices or vectors component-wise, or to raise all components of one matrix to the same power, rather than using matrix definitions of these operators, you can use the dot (.) operator. The two matrices must have the same dimensions. For example, for multiplication,

>> a = [1, 2, 3];
>> b = [0, 1, 2];
>> a .* b

ans =

  0    2    6

The other two componentwise operators are ./ and .^.

As matlab is a numerical computing language, you should keep in mind that a matrix which is theoretically invertible may lead to precision problems and thus giving imprecise results or even totally wrong results. The message above "matrix is singular to working precision" should appear in those cases, meaning the results cannot be trusted.

Non-square matrices can also be used as the right operand of /; in this case, it computes the pseudoinverse. This is especially useful in least square problems.

Transpose

A transpose of a matrix is taken using .'

 >> array = [1,2;3,4]
 array =
    1     2
    3     4
 >> array.'
 ans =
    1     3
    2     4

Boolean Operators on Arrays

The same boolean operators that can be used for point values can also be used to compare arrays. To do this, MATLAB compares the elements componentwise and returns them in a logical array of the same size as the two arrays being compared. The two arrays must have the same size. For example,

 >> A = [2,4], B = [1,5];
 >> A < B
 
 ans =
    [0    1]
 

You must be careful when using comparisons between arrays as loop conditions, since they clearly do not return single values and therefore can cause ambiguous results. The loop condition should be reducable to a single boolean value, T or F, not an array. Two common ways of doing this are the "any" and the "all" functions. A function call any(array) will return true if array contains any nonzero values and false if all values are zero. It does the comparisons in one direction first then the other, so to reduce a matrix you must call the any function twice. The function all, similarly, returns true if and only if all elements in a given row or column are nonzero.

Concatenating Arrays

Concatenating arrays involves sticking arrays together.

Horizontal Concatenating

Horizontal concatenation is done by treating an array as if it were a variable included in a row.

 >> a = [1,2;3,4];
 >> b = [5,6;7,8];
 >> c = [a,b]
 c =
    1     2     5     6
    3     4     7     8

Vertical Concatenating

Vertical concatenation is done by treating an array as if it were a variable included in a column.

 >> a = [1,2;3,4];
 >> b = [5,6;7,8];
 >> c = [a;b]
 c =
    1     2
    3     4
    5     6
    7     8

Solving Linear Systems

To solve a linear system in the form Ax = b use the "\" operator.

Example:

>>A = [4 5 ; 2 8];
b = [23 28]';
x = A\b

x =

     2
     3